从模拟滤波器传输公式到数字滤波器算法转换
从模拟滤波器传输公式到数字滤波器算法转换
信号滤波器最早都是基于模拟设计,如巴特沃斯,切比雪夫,贝塞尔滤波器。今年来由于数字系统的兴起,越来越多的模拟滤波器被数字滤波算法所替代。然而,虽然上述模拟滤波相对过时并且相较于数字滤波难以精确设定通带与中心频率,但是模拟滤波设计思想相对成熟。于是使用转换公式将模拟滤波器转换为数字滤波算法,即节省了设计验证的时间又将经典滤波器的设计沿袭下来。是现代数字滤波的一种设计思想。
由于模拟滤波器处理的信号为连续信号,其传输公式应从连续信号与连续傅里叶变换的角度来考虑,于是可用以下公式来概括常见模拟滤波的传输
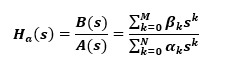
其中α与β均为输入与反馈系数,也由此可见模拟滤波器与IIR数字滤波器具有类似形式。一个滤波系统不单可由上式的滤波系数来描述,还可从冲击响应的角度来描述。如下式
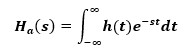
其中h(t)为一输入信号的时间域表示,H(s)为此信号的频域表示,两者通过连续信号傅里叶变换进行联结。最后,一个模拟滤波器的系数方程还可表示为时间域方程。如下式
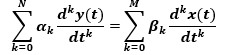
由上式,在时域表示上,模拟滤波也与数字滤波的形式类似。基于上面三个公式可使用三种方法对模拟滤波器公式进行变换:导数不变法,冲击不变法,和双线性变换。其中冲击不变法与双线性变换使用较多。
如使用冲击不变法对一模拟滤波器进行变换。假设此滤波器具有以下传输公式
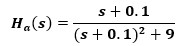
从上式中可发现极点为p=-0.1±3j,于是上式可拆分为
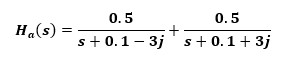
假设一数字系统的采样周期为T,则可写出以下等效数字滤波算法确保极点相同

合并后为
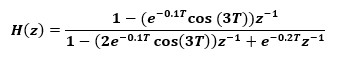
一个模拟系统还可使用双线性方法进行变化,如一个一阶模拟滤波器具有以下公式
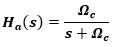
其中Ωc为3dB带宽。假设对应的数字滤波器具有0.2π的2dB带宽,则可建立以下联系。
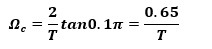
由上式可见Ωc与采样周期T的联系,于是将上式代回可发现
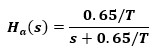
使用双线性变换公式
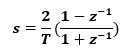
可变换为
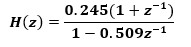

 服务热线:
服务热线:
