在数字信号处理的过程中，模拟信号经过采样与ADC从连续的模拟信号变为离散的数字信号。然后这些离散的数字信号通过运算单元经过卷积运算将时域信号变为频域并与滤波器参数进行卷积。最终的输出频域信号通过逆卷积再次回到时域信号并进行重建运算。其中的变换过程如下式

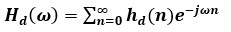
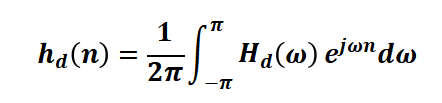
在上式中，eq.1为傅里叶变换，eq.2为傅里叶逆变换。从eq.1与eq.2中可以发现，傅里叶变换是基于无穷长度的冲击响应h(n)，而在真实的数字系统中内存的长度是有限的。比如，在处理一段声音信号时，需要对此声音信号在时域的所有波进行傅里叶变换。但是如果此信号是通过麦克风进行实时录入，我们是不知道未来的信号是什么的。因此，这个难题可以通过在数字处理系统中通过“加窗”对一个时段的信号进行傅里叶变换来进行处理。

通常的方法是对采样点的截取，例如用n代表采样点的编号，一个加窗函数截取长度为n=M-1个点，则此函数可表示为

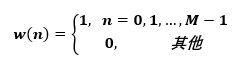
                      eq.3

当使用此窗函数截取一段时域信号h_d(n)时，卷积运算为

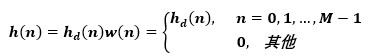
          eq.4

因信号处理系统是基于频域信号H_d(ω)与W(ω)的卷积，对eq4的时域信号进行离散傅里叶变换可发现

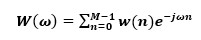
                      eq.5

通过观察eq3可发现，此窗函数为一方波，通过eq.5可写出此窗函数在频域的表达式

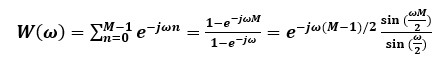
          eq.6

Eq.6又称“矩形窗”。

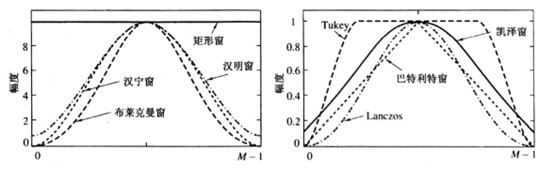
利用同样的设计原理，可设计多种近似矩形的窗函数通过频域卷积对时域信号进行截取。如“汉宁窗”

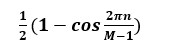
                               eq.7

“布莱克曼窗”

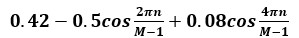
                    eq.8

窗体函数对信号处理不可同时兼顾通带带宽与旁瓣峰值，如“矩形窗”的带宽可设计的很窄以达到精准滤波，但是旁瓣峰值较高导致输出信号的信噪比较低。因此针对不同输出信号需求选择合适的窗函数变得重要。如下图中在时域对比了不同窗函数。

下图为一矩形窗中M不同时对应的不同频域波形，可以发现截取长度越长参数越多，相对应的性能越理想。

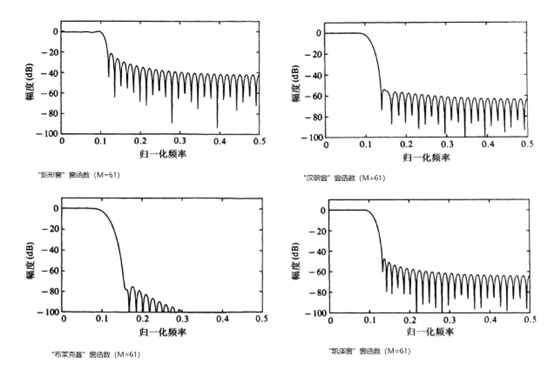
下图展示了四种窗函数当长度相同时的不同频域表现。由下图可见“矩形窗”具备较高滚降，但是通带波纹与旁瓣峰值较差。而“汉明窗”的通带波纹较低，“布莱克曼窗”的旁瓣峰值较低。