数字信号处理算法离散时间傅里叶变换与N点离散傅里叶变换

在数字信号处理DSP系统中，信号通过采样器，模数转换器（ADC）后进入数字处理系统进行计算。在这个过程中，虽然输入信号为模拟连续量，但是经过采样后的信号为离散的点。因此在DSP系统中，信号的处理基于离散傅里叶变换与逆离散傅里叶变换。其中一个离散信号可被表示为傅里叶级数DTFS。当给定一个周期为N的离散信号x（n）时，对于所有x（n）=x(n+N)来说，这个信号可被表示为由N个谐波组成的函数

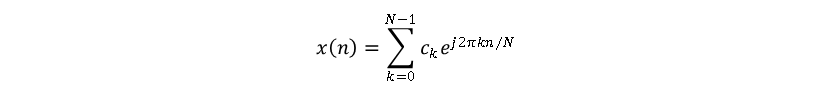
其中x(n)为一个离散信号，c_k为信号分量的系数，为信号分量，N为函数周期。基于傅里叶级数的原理，一个信号的频谱也可被表示为多个谐波频谱的组合函数。而对于离散信号在频域与时域间的变换称为离散时间傅里叶变换DTFT与逆离散时间傅里叶变换IDFT

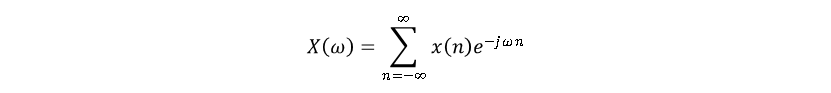
其中为此信号的频谱，而x（n）为输入的离散信号，为多个频率分量。基于此式还可写出逆离散时间傅里叶变换IDTFT。

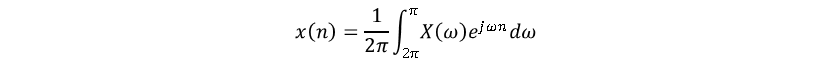
由上式可见当DSP系统输入信号为有限长度信号时，此信号频谱通常为无限长度。

一个DSP通常通过DTFT算法，将输入信号在频域与数字滤波器进行卷积。再通过IDTFT将滤波结果在频域变换到时域，从而产生信号处理结果。由上式可见，对于一个有限长度的信号来说，其频谱信号通常为无限长度。但是对于一个数字计算系统如MCU,FPGA来说，存储空间都是有限的。因此DTFT与IDTFT虽然在理论上成立，但是在现实中不可实现。因此为了将数字滤波算法应用于实际的数字计算系统，DTFT算法被简化以便于使得被处理信号在时域与频域都只有有限长度，以便于在有限的储存空间中进行处理。因此具有固定长度L的离散傅里叶变换DFT与IDFT被采用。

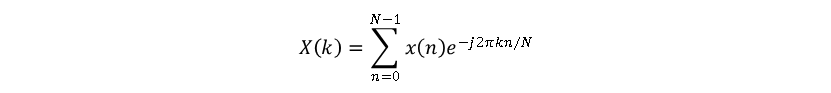
或此式可被表示为

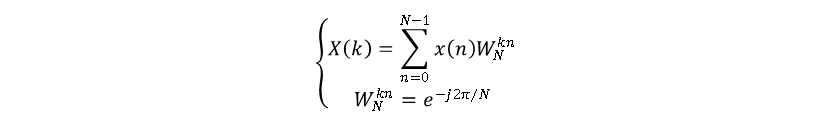
由上式可见，输入信号频谱具有了有限长度。第一个频率元素为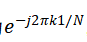

，而最后一个频率元素为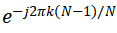。而其中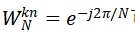可由计算机提前计算完成，计算时可通过查表简化计算。因此，在信号输入时可采用DFT算法将信号在频域内表现为有限长度频谱信号，虽然在逆变换后的信号因频谱丢失会有所失真，但在指定长度0~N-1范围内仍为有效信号。